Fract-ol: A Dive into the World of Fractals and Computer Graphics

Project Overview

Fract-ol is a captivating exploration into the beauty of fractals and the fundamentals of computer graphics. Developed in C using the MiniLibX graphical library, this project serves as an introduction to rendering visually stunning fractals, offering a blend of mathematical theory and graphical artistry.

Technical Foundation

Understanding Fractals

Fractals are intricate mathematical structures that exhibit self-similarity across different scales. Coined by Benoit Mandelbrot in 1974, the term originates from the Latin word fractus, meaning "broken" or "fractured." Fractals like the Mandelbrot and Julia sets are fascinating due to their infinite complexity and aesthetic appeal.

Key Technical Achievements

Rendering Capabilities

Fractal Types Supported:
- Mandelbrot Set
- Julia Set (with multiple parameter variations)
- Burning Ship Fractal (and its Julia variant)
Dynamic Features:
- Infinite zooming functionality
- Smooth color gradients to represent fractal depth
- Support for psychedelic color effects and custom palettes
- Interactive parameter manipulation via command-line inputs

Graphical Management

Seamless window handling:
- Smooth interactions like minimizing and restoring
- Clean and efficient program exit with ESC or window close actions
Mouse-based zoom and keyboard navigation for exploring fractals

Implementation Details

Mathematical Principles

The fractals are generated by iterating complex mathematical equations, such as:

Mandelbrot Set Equation:

$z_{n+1} = z_n^2 + c$

Where $z_0 = 0$ and $c = x + iy$ (the pixel’s coordinates in the complex plane).
Julia Set Equation:
$z_{n+1} = z_n^2 + c$
Where $z_0 = x + iy$ and $c$ is a constant defining the specific Julia set.

Points are colored based on the number of iterations before divergence (i.e., when $|z| > 2$ ).

Features and Options

Command-line options for customizing rendering:
- Center point, zoom level, and maximum iterations
- Selection of fractal types and color palettes
Responsive user interactions:
- Zooming with the mouse wheel
- Panning via arrow keys
- Real-time recalculations for parameter adjustments

Bonus Features

Additional fractals beyond the mandatory sets
Zooming centered around the mouse position
Dynamic color shifting for mesmerizing visual effects
Optimized algorithms for smoother rendering and interaction

Technologies Utilized

Programming Language: C
Graphics Library: MiniLibX
Mathematical Tools: Complex numbers and iterative algorithms

Usage

The program accepts various command-line parameters to customize the fractal rendering. Example:

./fractol <set> [-c x y] [-z number] [-m number] [-p palette] | [-h | --help]

Examples

Display Mandelbrot set:
```
./fractol mandelbrot
```

Render a Julia set with custom parameters:

./fractol julia -c -0.7 0.27015 -z 2 -m 1000 -p lsd

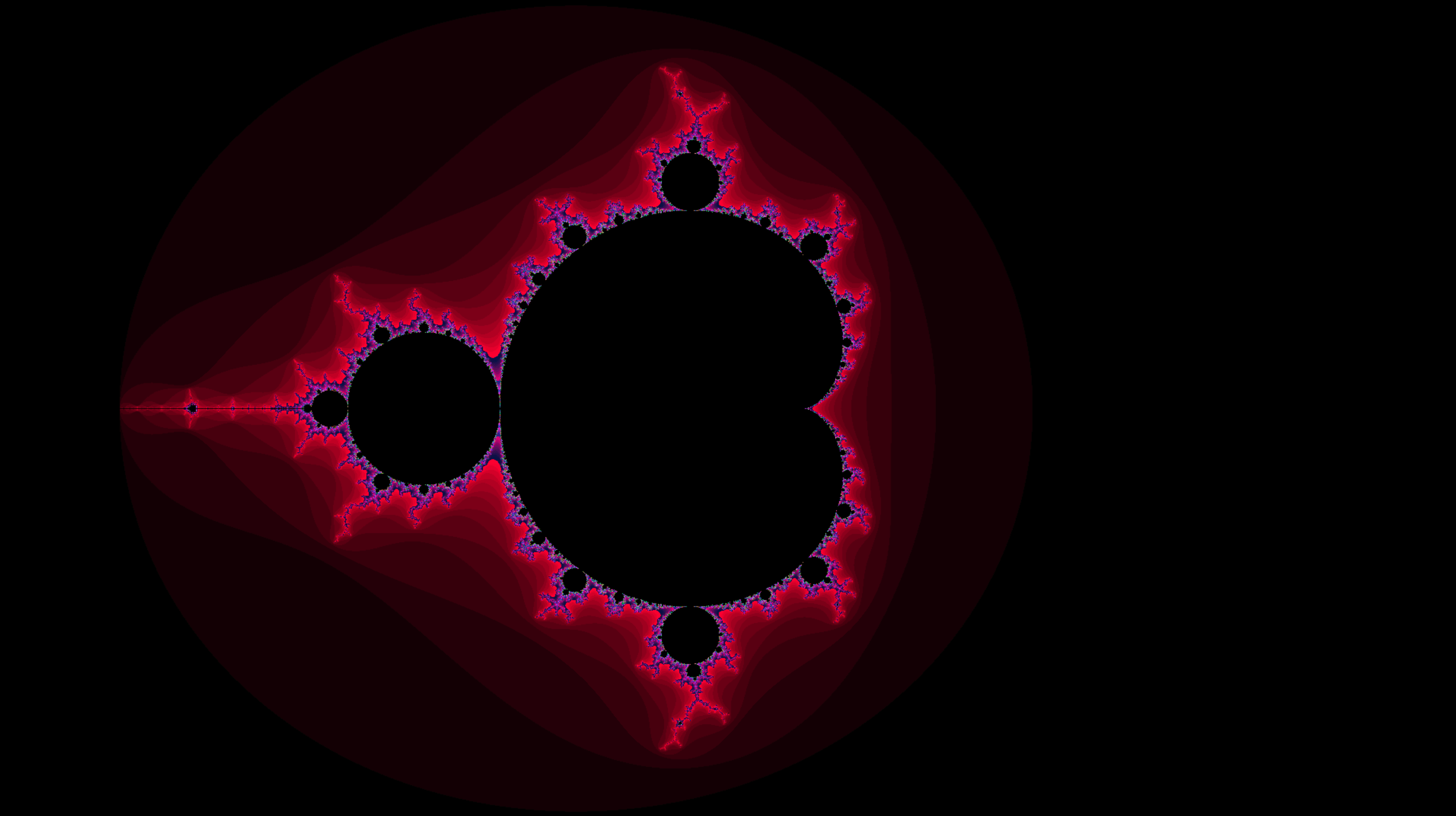
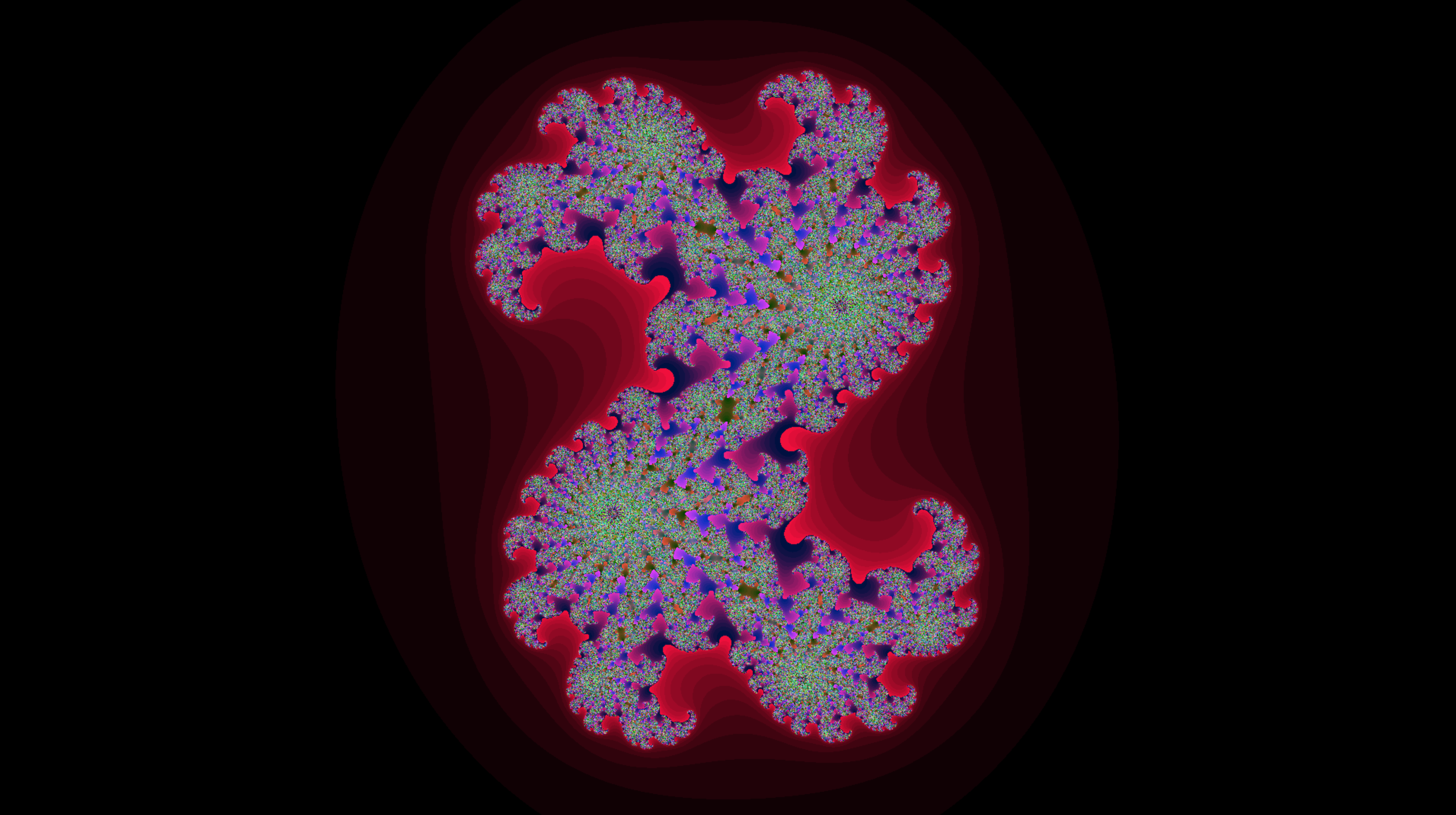
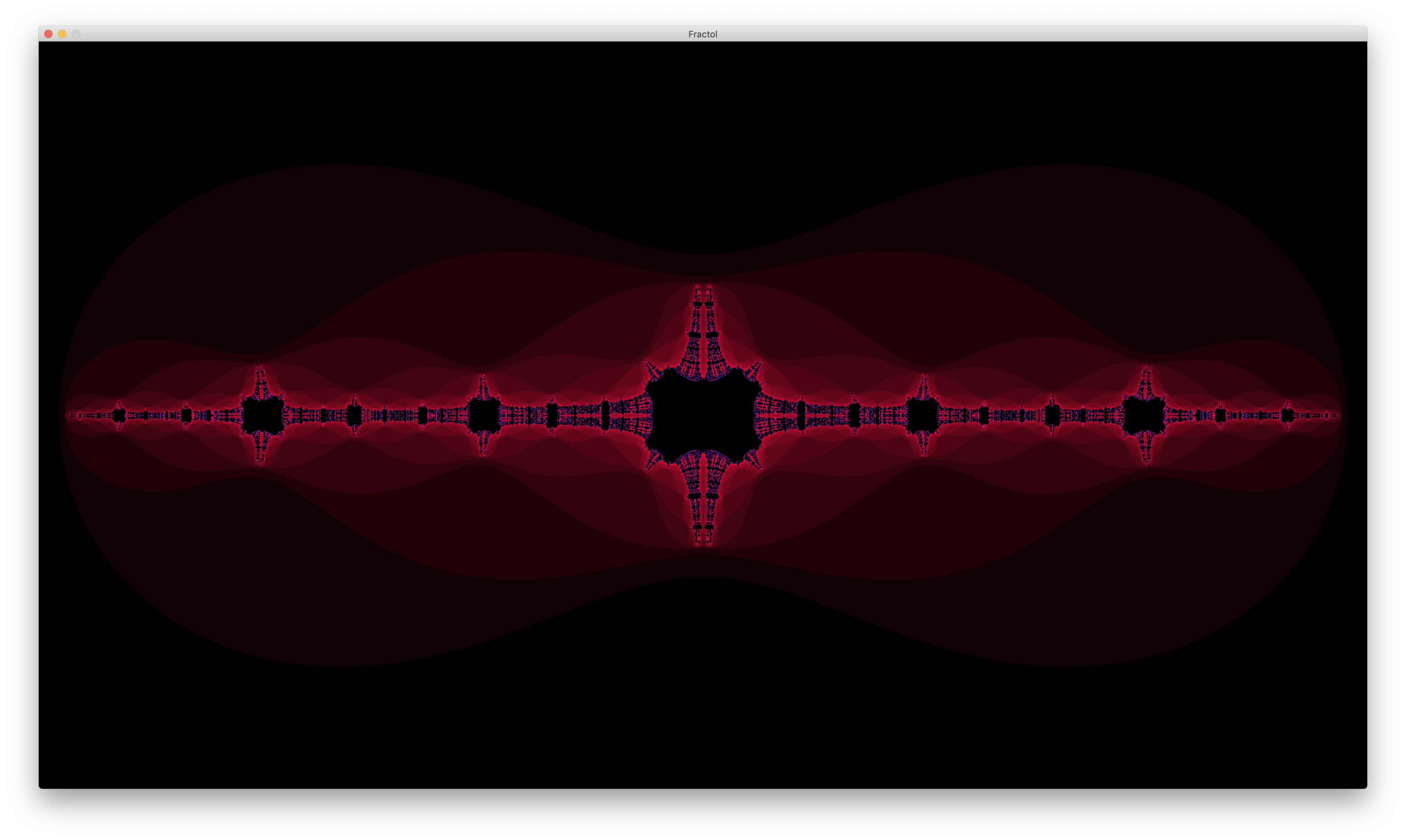
Visual Showcase

mandelbrot

mandelbrot

Julia lsd

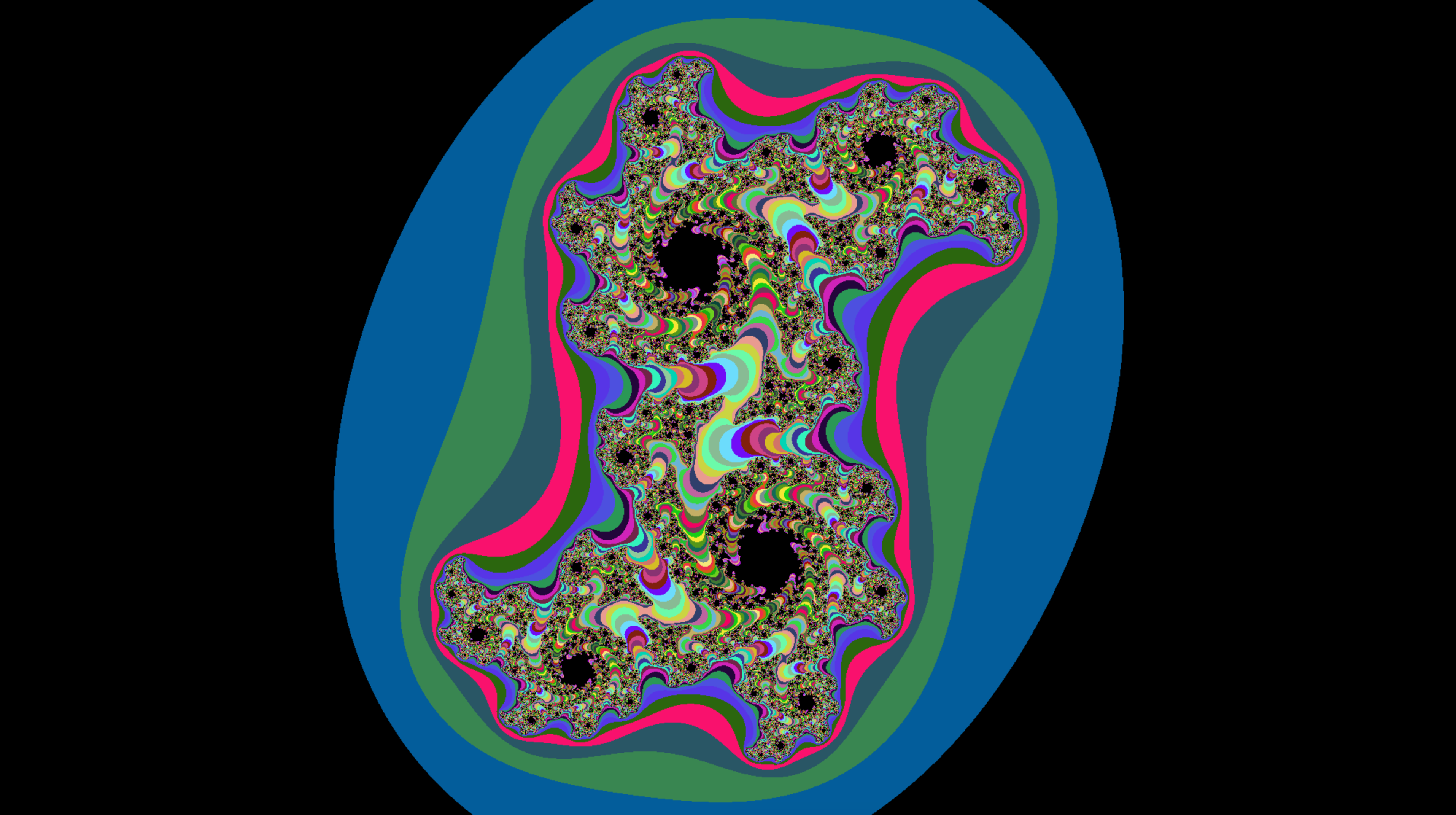
julia_lsd

Julia trip

julia_trip

burningship

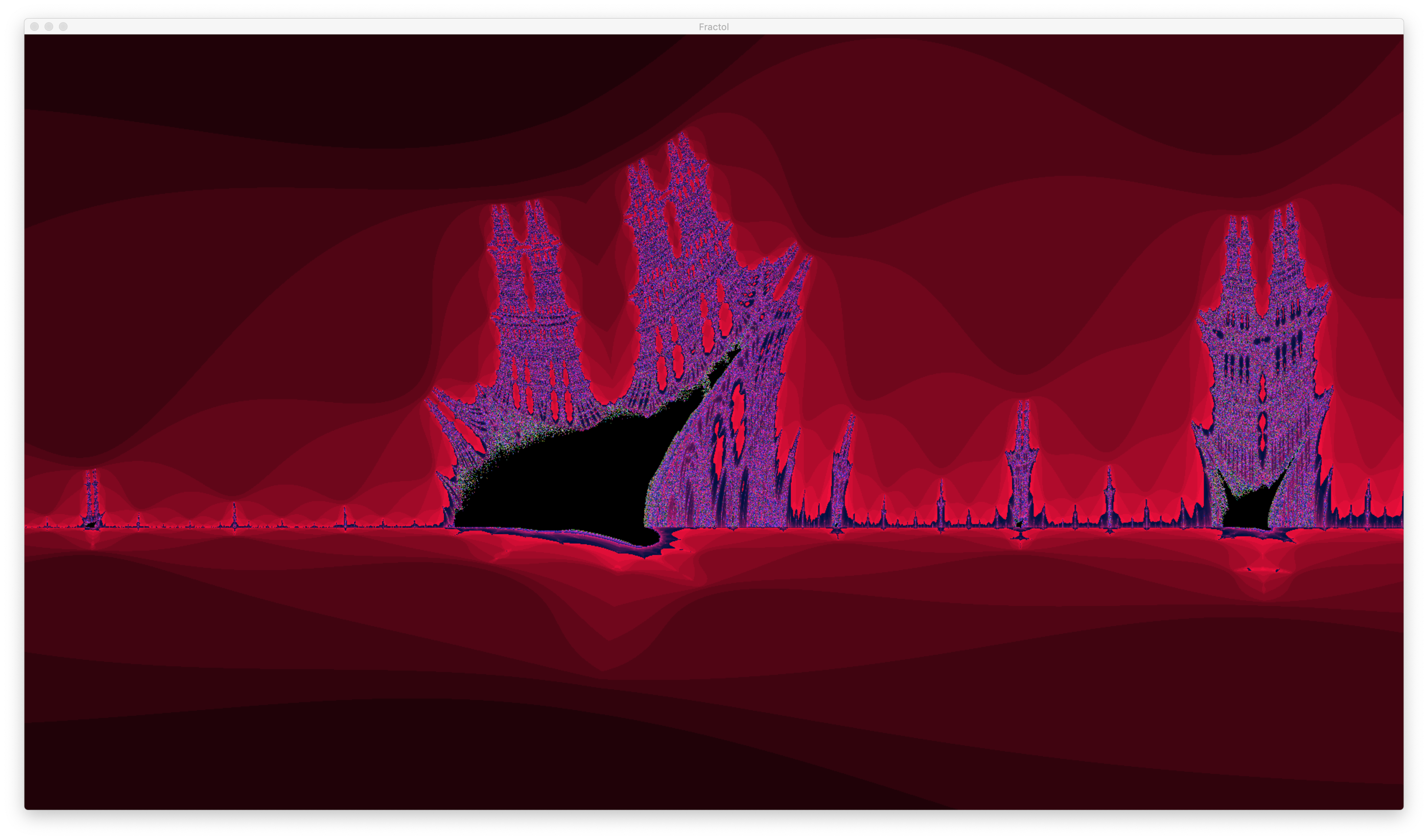
burningship

burningship julia

burningship_julia

Project Significance

Fract-ol is an engaging introduction to:

Mathematical modeling with complex numbers
Low-level graphics programming
Real-time rendering and interactivity in computer graphics

GitHub Repository

Explore Fract-ol on GitHub

Fract-ol combines rigorous programming with artistic expression, creating a mesmerizing display of fractal beauty while deepening your understanding of computer graphics.